Chaos theory and nonlinear dynamics
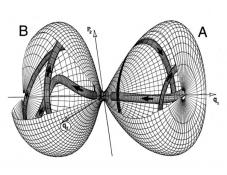My doctoral thesis at Yale was focused on the use of "chaos theory" (the theory of nonlinear dynamical systems) to understand chemical reaction dynamics at the molecular level. In the process, we found that phase space cylinders ("cylindrical manifolds" separate trapped motion from reactive motion and control transport across potential energy barriers. We used the discovery to develop a microscopic reaction rate theory for unimolecular processes which is more accurate than RRKM/transition state theory, accounting not only for recrossing but also for "clogging" of the return cylinders and the exclusion of trapped trajectories from the reactive flux. This work was directed by Nelson De Leon and was executed collaboratively with M.A. Mehta, based on earlier work by De Leon with C.C. Marston and Alfredo O. de Almeida. The image above was created by Mehta and illustrates the phase space dynamics of the DeLeon-Berne Hamiltonian. This was the first graphical numerical reconstruction of cylindrical manifolds.
This early work on cylindrical manifolds in phase space has impacted the fields of aerospace engineering, the celestial three-body problem (Lagrange points), and space mission design. See work by Shane Ross (Virginia Tech).
A recent paper (click here) shows how the theory can be extended to time-dependent Hamiltonians as well. See below for several publications. Brilliant work on these ideas is being done by Stephen Wiggins and his group (University of Bristol).
The dynamics of the De Leon-Berne Hamiltonian may be explored interactively online. See M. Hammond and N. De Leon, "Double Well Reaction Dynamics," , Published May 11, 2012. Link To Wolfram
In a separate project, more recently we have worked collaboratively with Song Ling in a study of semiclassical limits for molecular dynamics (see below).
References:
(1) S. Ling and R.Q. Topper, invited book chapter, On the zero point energy difficulty of quasiclassical trajectory simulations, in Handbook of Computational Chemistry Research, C. T. Collett and C. D. Robson, Eds., Nova Science Publishers, Hauppauge, NY, pp. 467-476 (2010). ISBN: 978-1-60741-047-8 . 2010LingTopperQuasiclassReprintLowRes
(2) R.Q. Topper, Visualizing molecular phase space: Non–statistical effects in reaction dynamics, invited article, in Reviews in Computational Chemistry10, pp. 101-176, K.B. Lipkowitz and D.B. Boyd, Eds., VCH Publishers, New York (1997). This is a review article and includes some of the content that was intended for III. in the series below (which never saw print due to battles with the referees over I and II). See also references therein. A preview is available on Google Books. Photocopy available on request. Link
(3) N. De Leon, M.A. Mehta, and R.Q. Topper, Cylindrical manifolds in phase space as mediators of chemical reaction dynamics and kinetics I. Theory,Journal of Chemical Physics 94, 8310 (1991). 1991_DeLeonMehtaTopper11
(4) N. De Leon, M.A. Mehta, and R.Q. Topper, Cylindrical manifolds in phase space as mediators of chemical reaction dynamics and kinetics II. Numerical considerations and applications to molecular models with two degrees of freedom, Journal of Chemical Physics 94, 8329 (1991). 1991_DeLeonMehtaTopper20
Also see: