Systems Engineering (ESC251)
ESC251 (formerly ESC161) Course Description: An introductory course to the mathematical modeling of systems. Topics include mechanical elements and systems, electric circuits and analogous systems, fluid elements and systems, analysis of systems using transfer functions, state space equations, analog simulation and digital simulation. Also covered are block diagrams, Laplace transforms, and linear system analysis. Computer projects will be assigned that will use MATLAB software. 3 credits. Prerequisite: Ma240
Topics:
- Differential Equations
- Laplace Transforms
- Stability
- Mechanical System Modeling
- Electromechanical Systems
- Block Diagrams
- State-Space Representation
- Linearity, Superposition, and Linearization
- Fluid and Thermal Systems
- Transient and Steady-State Response
- Time Domain Specifications
- Introduction to Feedback Control
- Computer methods for analysis and simulation of dynamic systems
Systems Engineering (ESC161) is the first course in a two-course sequence required for mechanical engineering majors. This course is an introductory course to the mathematical modeling of systems. The modeling of systems is an interdisciplinary skill and the course attracts engineering students from outside the ME department. Students learn how to model a variety of systems, including mechanical, electrical, fluid, thermal, and mixed systems, such as electromechanical, and solve for the system’s response using differential equations and Laplace Transforms.
Numerical modeling and analysis methods and MATLAB/Simulink are widely used in research and industry. ESC161 students partake in a week-long MATLAB/Simulink seminar and are assigned a tutorial and MATLAB/Simulink assignment. For many, these MATLAB skills prove very useful in summer internships or their first jobs and/or for modeling and data analysis in subsequent research projects.
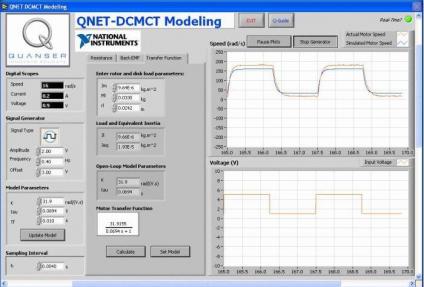
To help students relate to theory they are leaning, students spend time in the Mechatronics Laboratory on a National Instruments Educational Laboratory Virtual Instrumentation Suite (NI ELVIS) and Quanser Engineering Trainer (QNET) DC Motor Trainer. Using these trainers, students derive an experimental model for a DC motor and then compare the actual system to the analytically determined system gain and time constant and simulation results.